Purpose

This document describes a number of new inventions relating to the production of music, particularly for electronic keyboards. Many of these inventions relate to the frequencies of the notes produced and the result removes the need to make compromises that have existed for many centuries.

Background

Since the time of Pythagoras there has been debate about the correct relative frequencies of different notes in the musical scale. There have been many different ways of tuning instruments such as pianos where the frequencies of notes are preset, as distinct from instruments like violins where the notes may be individually controlled while playing. Compromises where made so that more than one key could be played in, although even in any one key there are some debatable frequency relationships. Bach is often credited with popularising the modern equitempered scale which is really a compromise between all the different keys. The use of the equitempered scale has been so accepted for so long that it is not often questioned today, which can be expected to lead to some negative reaction to the current proposals. There are some instances however where the tuning of keyboard instruments is recognised as a problem, including when they are played with stringed instruments that are accustomed to making perfect harmonies. A chord on a piano is normally not a perfect harmony, and stringed instrument players and singers must make compromises about which note on the piano to harmonise with.

Equitempered scale

The equitempered scale is based on an octave having 12 semi-tones of exactly equal ratios. The ratio used is therefore the 12th root of 2, or 1.0594631. This leads to the notes of the chromatic scale having the following relative frequencies:- 
  C    C#   D    D#   E     F    F#   G    G#   A    A#   B     C

1.000     1.122     1.260 1.335     1.498     1.682     1.888 2.000
     1.059     1.189           1.414     1.587     1.782
The upper line contains the notes of the key, while the lower line has the notes not belonging to the key (i.e the black notes when in C).

The Compromise

While it is the case that 12 is the best low number to divide the scale into in this manner. looking at specific ratios will show the in built discrepancies. Assuming that the key is C, then let us look at the important chords.

Firstly the Major chord is C-E-G. Ideally the notes are in the ratio 4-5-6 or 1-1.25-1.5 but the equitempered scale has 1-1.260-1.498. The difference of 1.498 from l.5 is probably only able to be detected by the very best musical ear, but the variation of 1.260 from 1.25 is noticeable though small. This chord sounds very close to correct.

Next, if we add the note A# to make dominant 7th chord, we have, C-E-G-A# which has relative frequencies of 1-1.260-l.498-1.782 while the ideal ratios are 4-5-6-7 or 1-1.25-1.5-1.75. The difference of 1.782 from 1.75 is very noticeable. and results in quite a strained sound. Part of the strain is due to using the ratio 7 which is less pleasing than 4 and 6 (more about this letter) but, much is due to the wrong frequency being used. It is true that composers use these differences for effect also, and so may not always want the ideal frequencies. It is also true that they cannot get the ideal frequencies even if they do want them.

The Invention

The basic idea of the invention is that with modern technology it is no longer necessary to make compromises. Modern electronic keyboard instruments could easily incorporate the extra logic and functions to make perfect chords all the time. It is not difficult in most cases to calculate from a set of notes being played simultaneously (a chord) what the exact frequency ratios should be to make the most harmonious sound. It is also necessary to determine the relationships between the frequencies in a chord and those in a previous chord. While this is often simple and clear, there are cases that are ambiguous or complicated, and it is desirable to include some options so that the player of the keyboard can indicate their preferences. The difficult cases occur mostly when unusual key changes are made. It is possible that some composers works are more easily dealt with than others, and it is also intended that the feature can be turned off and on, and that an additional option will allow the keyboard to be set up in a fixed key. All of this is explained in greater depth below.

Some Definitions

Fundamental Frequency and Fundamental Note: The highest common factor of the ideal frequencies in a chord. The note with a frequency ratio of 1 when the frequency ratios of all the notes are reduced to the smallest whole number ratios. For example if the major chord C-E-G is played, the frequency ratios are 4-5-6, so the fundamental note with frequency 1 is the C two octaves below the C in the chord. The fundamental frequency is the frequency of that note.

Ideal Harmony: Having notes (in a chord or sequence) in perfect harmony, which means the frequencies are in (generally) small number ratios. For example for a major chord the ratios are 4-5-6.

Note Number: The notes are numbered, starting at zero on some note and going up one for each semitone. For example the C with a frequency of (about) 8 Hz could be note zero. Then middle C would be note number 60 because it is 5 octaves of 12 semitones/octave higher. The E above middle C would be note number 64 because it is 4 semitones higher.

Basic Scale Frequencies: The 7 notes of any one key have frequencies which are certain exact multiples of the key note. These ratios are shown:- 

Note:     do  ray me  fah soh lah ti  doh
Multiple: 1   9/8 5/4 4/3 3/2 5/3 15/8 2
Ratio:    24  27  30  32  36  40  45   48
All of the above can be derived from the major chord ratios being 4-5-6 They derive from 3 chords, doh-me-soh, soh-ti-ray and fah-lah-doh.

Principles of Design

1. The frequency of every note may vary according to circumstances.

2. Frequencies may vary to achieve ideal harmony within a chord.
(Set of simultaneous notes)

3. Frequencies may vary to achieve ideal harmonic progression.
(Set of Successive notes)

4. Frequencies may vary according to the key being played in, which may be indicated by some special means.

5. Chords may be achieved which were not really available previously, for example proper 7th chords which were previously a poor compromise.

6. The key may be kept track of and used to provide (additional) accompaniment.

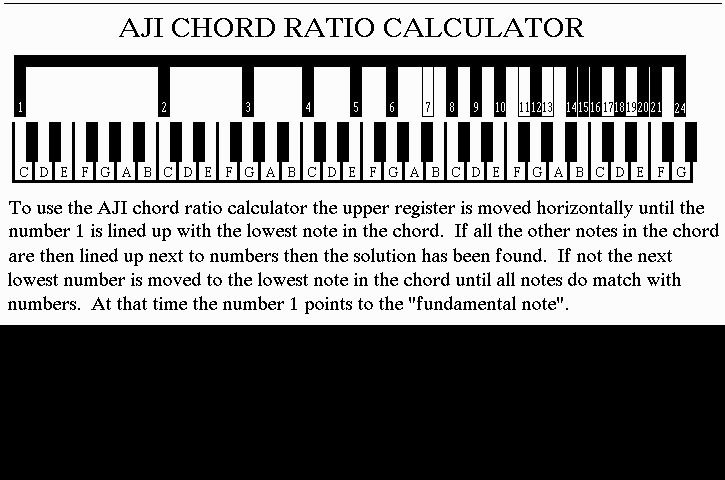
7. The key may be kept track of by finding harmonies in chords and successive notes and working out the fundamental note.

Ratio Note Finder

This is a device for finding the ratios that the frequencies should have given a set of notes. A simplified version can be constructed by printing this graphic and cutting it into two pieces to make a chord ratio calculator. 

Note No. 0 12 19 24 28 31 34 36 38 40 42 43 44 46 47 48
Ratio    1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
For ratios above 16 some notes have several possible ratios. The best ratio is given as well as the possible range. 
Note    49   50   51   52   53   54   55   56   57   58   59   60
Best    17   18   19   20   21   22   24   25   27   28   30   32
Range                            22-       25-       28-  30-
                                 23        26        29   31

Note    61   62   63   64   65   66   67   68   69   70   71   72
Best    33   36   38   40   42   45   48   50   54   56   60   64
Range   33-  35-  37-  40-  42-  44-  47-  50-  53-  56-  59-  63-
        34   36   39   41   43   46   49   52   55   58   62   65

Note    73   74   75   76   77   78   79   80   81   82   83   84
Best    66   72   75   80   84   90   96  100  108  112  120  128
Range   66-  70-  74-  79-  83-  88-  94-  99- 105- 111- 118- 125-
        69   73   78   82   87   93   98  104  110  117  124  131
For higher values, continue to double the best values of the last line.

The above table shows for each ratio how many notes (semitones) the interval needs to be. Note that above note 46 all note numbers are present but above ratio 21 not all ratios are present (as best values).

The table is used as follows. Take any set of notes (chord or series) and count the lowest note as note 0 numbering the rest from there (eg C-E-G would be 0-4-7) then see if these numbers are in the above table. If they are not ALL present then add one to each of them and look again. Repeat this procedure until they are all present. At this point the fundamental note is the note with note number 0 taking the notes in the set as the final values after all the l's have been added. (e.g. for our C-E-G above we had 0-4-7 which are not all present, and we must add 1 a total of 24 times to get 24-28-31 before all the numbers are present in the table. This corresponds to ratios 4-5-6 and also tells us that the fundamental note is C 24 semitones or two octaves below the C in the chord).

An optional alternative is to not include the ratios 7, 11, 13 and possibly other higher prime numbers. This allows for possibly finding a better fit for some chords. If the chord has no better fit it will still find the ratio but with the numbers doubled (e.g. 7-9-11 will be found as 14-18-22) and the numbers may then be divided by two.

Variations on Ratio Note Finder

a. As listed. The first ratio found that matches all notes played.

b. As listed except that certain numbers are not included as ratios, these being all prime numbers from 7 upwards.

c. The search of the ratio/note number table is not stopped when a match is found, but all matches (except those that can cancel) are found, then these are evaluated for the best one. This is done on a point scoring system and the patent includes the idea of point scoring. One possible points system is :-

1. For each possible solution found factorise all the ratios found for that solution.

2. Take the highest power of each prime in the factorisation and multiply it by a loading and add the results up to give a score. Some possible loading schemes are :- factor 

                      2    3    5    7    11   13  etc. Notes
          a. loading 1.39 3.30 8.05 13.6 26.4 33.3      n*log(n)
          b. loading 0.00 0.69 1.39 1.79 2.30 2.48      log(n-1)
          c. loading 0.69 1.10 1.61 1.95 2.40 2.56      log(n)
3. The possible solution with the lowest score is the one used. 
    Example:- Note numbers 24 26
    Method 1 gives ratios 7 8 for the frequencies.
    Method 2 gives ratios 8 9 for the frequencies.
    Method 3 considers the ratios 7 8 and 8 9 and 9 10 and others
      Factorising these gives 7 2^3 and 2^3 3^2 and 3^2 2*5 respectively.
      The highest power of primes in the order 2 3 5 7 for these cases
      are 3 0 0 1 and 3 2 0 0 and 1 2 1 0 respectively.
      Loadings a scores them 17.77 (3*1.39+13.6) and 10.77 and 16.04.
      Loadings b scores them 1.79 (3*0.00+1.79) and 1.38 and 2.77.
      Loadings c scores them 8.16 (3*0.69+1.95) and 4.27 and 4.50.
      In all cases the second option, ratios 8 9, is the best scoring.

Variation of ratios in ratio note finder table

Some ratios, most notably 25/26 35/36 38/39 44/45 63/64 80/81 (and others) would fall on the same note number causing ambiguity. In other cases one is clearly preferred such as 40 not 41 and 60 not 59 or 61. In cases with more than one possibility, optionally the calculation can be performed with all combinations to find the best solution. This may initially be unpractical, but as electronics speeds increase will likely become so. For example if ratios 3 4 24 35/36 occur then 36 is clearly correct, while for ratios 5 7 25 35/36 it is clear that 35 is better.

Consideration of when ratio calculation is performed

Whenever a new note is pressed (note on in MIDI terms) the calculation is performed using all notes that are now down. When a note is released (note off in MIDI) then no further calculation is done, but that note is no longer sounded. This method allows for the possibility that when a chord is played the notes are not likely to be pressed exactly at the same moment. It is possible that the frequencies will have some changes in the few moments between pressing the first and last notes of the chord, but this should not normally be noticeable.

Variation on notes included in ratio note finder

To better harmonise with a previous chord, the fundamental note (or optionally 12 or 24 notes higher than this) could also be included in the ratio note finder calculation. The resulting ratios excluding the previous fundamental would then be cancelled (reduced for common factors). The present fundamental note becomes the previous fundamental note whenever a note is released. Optionally, in consideration of notes played accidentally, if a note was held for less than a set time (e.g. 50ms) then this would not effect the previous fundamental note.

Finding the Fundamental Note

Given a set of notes, which may be either a chord or a sequence of notes such as an arpeggio, this section gives a method and variations for determining the Fundamental note of that set. The fundamental note has a frequency that divides exactly into the frequencies of all the notes in the set. The procedure under Ratio Note Finder above yields both the fundamental note, and the ratios of the notes in the chord. These give the exact ratios to be used when playing the chord. For example for C-E-G the frequencies sounded by the instrument will be in the exact ratios 4-5-6.

The Frequency of the Fundamental Note

The frequency of the fundamental note is not as straight forward as finding the ratios of the notes in a chord. Various schemes are possible, and each has advantages and disadvantages. Some possible methods are:-

1. Use the equitempered scale for the fundamental frequencies. This method may seem not to be in the spirit of the invention, but it has the advantage that small discrepancies do not accumulate (more about this) as is possible with some other methods. It is also easy to predict.

2. Base the basic scale frequencies. This depends on the key being declared beforehand. The method is technically more correct than 1, but declaring the key may be a nuisance.

3. Work out the key of the first chord (may be one note only) and then use its basic scale frequencies until a new fundamental indicates a key change. Future scale frequencies will be based on this scale until the next change. Each change will be based on the previous key, so that it is possible after several changes to return to the same key but NOT the same frequency.

4. The same as 3, but with a small factor to keep dragging the frequency back to the starting scale. A change of only 10% of the discrepancy towards the equitempered scale for each chord would prevent the discrepancy from growing to significant levels.

5. Use the frequency of the note in the scale of itself. This is the same as defining each key to be a frequency ratio of 3/2 to adjacent keys. Adjacent keys means keys with one more or less sharps or flats. The frequencies for the notes in the octave from middle C would be:- 

  C        Db       D        Eb       E        F
264.0000 278.1234 297.0000 312.8889 334.1250 352.0000

      F#/Gb         G        Ab        A       Bb       B
370.8313/375.8906 396.0000 417.1852 445.5000 469.3333 501.1875

Multiple Instruments

It is possible that several instruments of this type could be played together. Then, because they will likely play different note combinations they may not remain in perfect tune with each other. This could be overcome by connecting them together and combining all their notes in doing the chord calculations. This could be done through standard MIDI interfaces which provide all the information necessary.

Consideration of multiple instruments connected by MIDI

Although MIDI provides all the necessary information about note on and note off, it would be necessary to also have a command to prevent the instruments playing notes that were intended for calculation purposes only. The commands needed in MIDI are
1.Calculate only mode on.
2.Calculate only mode off.
Both these commands should ideally apply to the channel issued on. Initially they may need to be implemented by system exclusive command, but they should ideally be incorporated into the MIDI specification.

Frequency Variation Examples

A pair of notes may have a different ratio of frequencies according to what other notes are played with them. For example an interval of 2 semi.tones often corresponds to a frequency ratio of 8-9, but may be 7-8 or 9-10 depending on a third note, 
   Chord    A-C-D  G-C-D   F-C-D
   Ratios   6-7-8  6-8-9   6-9-10
If C had the same frequency in each of the above examples, then D would be a frequency of 64/63 in the first and 80/81 in the third relative to the middle example. These are the two most common variations of any note, and are noticeable, being about a quarter of a semitone.

Accompaniment

Because the keyboard now "Knows" what key is being played, it is possible to do an automatic accompaniment without having to press a note in the base for the key. The automatic key playing would follow the base note as well as recognise the most common recent base note as the actual key.

Enable Switch

A three way switch would enable or disable the automatic adjustment of note frequencies. The three settings would be:-
1. Equitempered scale. This would cause the keyboard to play notes of the frequency normally used now for all keyboards.
2. Set Key. This setting would take the first note played as the key to remain in, and use just intonation for that key.
3. Automatic. This setting would fully enable the features of this invention, automatically calculating the frequencies of all notes.

Non-electronic instruments

This invention could be implemented for other instruments such as pianos, although this is likely to be expensive. The expense may be worthwhile for concert instruments however. The method of implementation would be as follows:-

The piano (or other instrument) would still have the same electronics as described above for an electronic keyboard. It would also have pickups for each key to know what notes are played. Each string (or set of strings for one note) would have an adjustable stop near one end that was controlled by stepping motor to vary the effective length of the string (much like a human finger on a violin or guitar). The string would be sounded by the normal mechanism in the normal way. This device would also allow such effects as tremolo on a piano! There may well be problems to overcome in terms of wear on the string.

The detailed calculations for two small examples follow.

AJI Example 1

POLONAISE :-     Wolfgang Amadeus Mozart       in the key of F

Notes       Note        Ratios     Fundamental      Frequencies
Played      Numbers                Note Freq.         Played

F3 A3  C5    12 16 31    4  5 12    -12 F  44        176 220 528
   C4  F5       19 36       3  8      0 F  88            264 704
F3 A3  "     12 16 36    4  5 16    -12 F  44        176 220 704
   C4  A5       19 40       3 10      0 F  88            264 880 *
   "   G5       19 38       1  3     19 C 264            264 792
F3 A3  G5    12 16 38    4  5 18    -12 F  44        176 220 792
"  "   F5    12 16 36    4  5 16    -12 F  44        176 220 704
   C4  E5       19 35       2  5      7 C 132            264 660
   "   F5       19 36       3  8      0 F  88            264 704

E3 Bb3 C5    11 17 31    5  7 16    -17 C  33        165 231 528
   C4  G5       19 38       1  3     19 C 264            264 792
E3 Bb3 "     11 17 38    5  7 24    -17 C  33        165 231 792
   C4  Bb5      19 41       2  7      7 C 132            264 924
   "   A5       19 40       3 10 &    0 F  88            264 880 *
E3 Bb3 A5    11 17 40    5  7 27    -17 C  33        165 231 891 *
"  "   G5    11 17 38    5  7 24    -17 C  33        165 231 792
   C4  F#5      19 37       4 11 @   -5 C  66            264 726
   "   G5       19 38       1  3     19 C 264            264 792

F3 A3  A5    12 16 40    4  5 20    -12 F  44        176 220 880
   C4  A5       19 40       3 10      0 F  88            264 880
   "   F5       19 36       3  8      0 F  88            264 704
F3 G3  Bb5   12 14 41    8  9 42    -24 F  22        176 198 924
   C4  Bb5      19 41       2  7      7 C 132            264 924
   "   G5       19 38       1  3     19 C 264            264 792
F3 A3  C6    12 16 43    4  5 24    -12 F  44        176 220 1056
"  "   A5    12 16 40    4  5 20    -12 F  44        176 220 880
   C4  G5       19 38       1  3     19 C 264            264 792
   "   F5       19 36       3  8      0 F  88            264 704

. . .    continued

Notes

1.  All bar 1 frequencies are divisible by 44 and the key is always F, while
    bar 2 are all divisible by 33 and key is C (see note 3) and bar 3 all
    notes are divisible by 44 again.

2.  The items above with a "*" are all A, but sometimes the frequency is
    880 and at others 891.  See note 3 also.

3.  The item marked with a "&" has ratios 3 10, but under the alternative
    method (points for ratios) the ratios could be 8 27.  This would then
    make the fundamental be C and agree with the rest of the bar.  This A
    would then be frequency 891. The alternative method of note finder
    would certainly give 8 27.

4.  The item marked "@" has the ratios 4 11, and 11 is not very common.
    It seems that this was Mozart's intention as the fundamental is in
    keeping with the surrounding chords.  Another possibility is 16 45.

5.  The item marked "#" has a ratio 42.  If the variation of ratios feature
    was included, 42 and 43 would both be considered, and 42 chosen.

6.  All the frequencies are an exact number of Hz.

AJI Example 2

ROMANCE :- Ludwig Van Beethoven                  In the key of G

Notes          Note         Ratios      Fundamental    Frequencies
Played         Numbers                  Note Freq.     Played

B4             28           1           28 B 495       495
C5             29           1           29 C 528       528
D5             31           1           31 D 594       594

G3    G4       12    24     1     2     12 G 198       198        396
B3 D4 "        16 19 24     5  6  8    -12 G  49.5     247.5  297 396
B3 D4 G4       16 19 24     5  6  8    -12 G  49.5     247.5  297 396
F3    B4/A4    11    28/26  3     8/7   -8 B  61.875   185.6+     495/433.1+
C4 D4 G4       17 19 24     8  9 12    -19 C  33      *264    297 396
C4 D4 A4       17 19 26     7  8 12    -17 D  37.125  *259.9- 297 445.5

G3    B4       12    28     2     5      0 G  99       198        495
B3 D4 "        16 19 28     5  6 10    -12 G  49.5     247.5  297 495
B3 D4 G4       16 19 24     5  6  8    -12 G  49.5     247.5  297 396
B4             28           1           28 B 495       495
C5             29           1           29 C 528       528
D5             31           1           31 D 594       594

E3       G4     9       24  3        7 -10 A  55.6875  167+           557-
"  G3 B3 "      9 12 16 24  6  7  9 14 -22 A  27.844-  167+ 195- 251- 390-
"  G3 B3 G4     9 12 16 24  6  7  9 14 -22 A  27.844-  167+ 195- 251- 390-
E3     A4/G4    9    26/24  3      8/7 -10 A  55.6875  167+      445+/390-
"  G3 C#4 F#4   9 12 18 23 12 14 20 27 -22 A  27.844-  167+ 195- 278+ 362-
"  G3 C#4 G4    9 12 18 24  6  7 10 14 -22 A  27.844-  167+ 195- 278+ 390-

D3        A4    7       26  1        3   7 D 148.5     148+           445+
"  F#3 D4 "     7 11 19 26  4  5  8 12 -17 D  37.125   148+ 186- 297  445+
"  F#3 D4       7 11 19     4  5  8    -17 D  37.125   148+ 186- 297

. . . continued

Notes

1. At "*" C changes frequency from 264 to 259.9.  This is because C and D
   occur together in two successive chords but their relationship changes
   because of the third note changing from G to A.

2. The pattern of the fundamental note in this piece is very interesting
   going:- BCD GGG BCD GGG BCD AAA AAA DDD ...
   That this is so is not at all obvious from the score, with the second
   BCD having the same melody as the second AAA, but quite different to
   the first BCD.

3. The fundamental frequency is given to high accuracy but space limitations
   meant that the note frequencies are truncated.  The accurate frequencies
   can be derived from the fundamental times the ratios for each chord.

 Return to Ray Tomes index page