Reference: RT113
Date: 19-Dec-94
Author: Ray Tomes
Email: rtomes@kcbbs.gen.nz

Tomes Harmonic Theory predicts that there are especially
powerful standing electromagnetic waves of period near
160 minutes and 6 minutes, and that these should have a
major effect on all aspects of solar system formation.
This is shown to be the case, with effects on planetary
distances from the sun, planetary mass/radius relationships,
planetary rotation periods, and solar oscillations.

Keywords: Solar system formation, Planetary formation,
Quantisation, Harmonics theory, 160 minute oscillation,
5 minute oscillation

This paper applies Tomes Harmonic theory to the solar system.
It is more easily understood after reading 
RT103 "Harmonic
Theory Overview".  In essence, that paper explains how a
non-linearity in the universal law (a slightly different
interpretation to Maxwell's equations) will lead, because
of non-linearity, to a particular pattern of harmonics, and
this pattern accurately predicts the scale of all the more
prominent features of the universe, including galaxies, stars,
planets, moons, atoms and particles. At each scale there is
predicted to be strong tendencies to quantisation, and the
unit quantities are predicted to have certain common ratios,
especially 2, 12, 24 and other numbers with powers of 2 and 3.

Quantisation affects both distances and periods, with the
relationship between these being the speed of light.  The
important quanta in the solar system are 80 and 160
minutes and 3 and 6 minutes.  These should be related by a
ratio of 24, although the observed value is a little higher.

At the time of solar system formation, standing waves of
electromagnetism (and gravity) meant that planets could
form only at the nodes of these waves.  At other locations
the matter would be seriously disrupted.  Similarly, the
rotation periods of bodies, and their surface orbital periods
(the period of a satellite just above the surface) must also
fit in with the periods of the standing waves or planetary
formation would be disrupted.

Solar Oscillations.  There are many different periods in the
solar oscillations, but the two most prominent ones are the
160 minute oscillation and the (so called) 5 minute oscillation
(which is really a series from 3 to 8 minutes and a peak between
5 an 6 minutes).  There are other less powerful oscillations
clearly harmonically related to 160 minutes.  The meaning of
the 5 minute oscillations is the time it takes sound to bounce
around the sun in a variety of different oscillation modes.
As I understand it, no known mechanism exists for the 160
minute oscillation.  I propose that this period is the orbital
period of matter near the stellar surface, and that this is the
source of the oscillations.

Planetary distances. Bode's law has been proposed with a sort
of modified ratio between planetary distances.  Of course it
cheats in its series, and pretends there is a missing planet,
and omits Neptune altogether.  I suggest that the planetary
distances more nearly fit two arithmetic series than one
logarithmic one.  The outer four planets are all near multiples
of 10 au (astronomical units) with Jupiter at half that, and
the inner ones are near multiples of 0.36 au.  These planetary
waves are shown in the figure below.



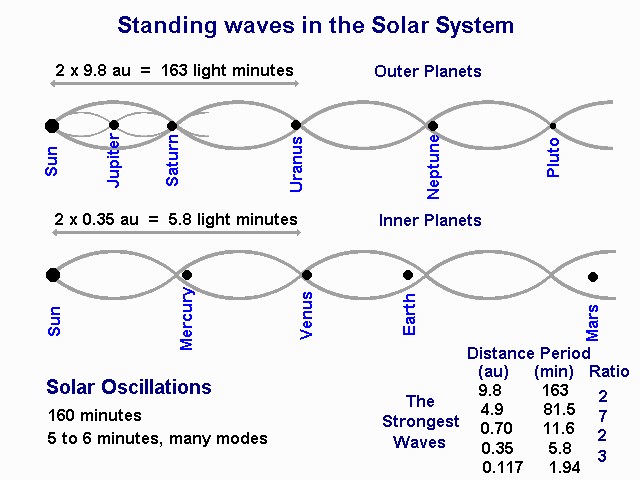
Consider now the meaning of these distances.  In light time,
10 au is 83 minutes and 0.36 au is 3 minutes.  Doubling these
gives 166 minutes and 6 minutes.  The doubling relates to the
fact that nodes of standing waves occur at half wave intervals.
These values agree well with the solar oscillation periods.
Is this coincidence?  If you think so, then get ready for some
more.

The orbital period of a satellite just above the surface of
a planet is closely related to the density of the planet.
For the major bodies in the solar system it has the following
values.  For Mercury, Venus and Earth, all a little over 80
minutes.  For the Sun, Jupiter, Uranus and Neptune all a little
over 160 minutes, and for Saturn a bit over 240 minutes.
Mars is the only planet not near a multiple of 80 minutes.
I propose that at the time of planetary formation (and solar
formation) these bodies actually had the orbital period as
their rotation period. This means that any additional matter
could not settle.  Since then tidal forces have altered the
rotation periods.  Those planets with no moons now must have
lost them due to tidal action moving the moons away as the planets
rotation was halted.

The rotation periods of planets.  Some planets have rotation
periods which are n^2 x 160 minutes, and others n^2 x 6.4 days.
This is quite similar to quantum spins in atomic phenomena.
I don't know exactly why the value is n^2 rather than n.
In the above, n is a small integer.  For Pluto, the Sun,
Mercury and Venus, n is 1, 2, 3, and 6 with the 6.4 day
constant, while n is 2 for Jupiter and Saturn, and 3 for
Earth and Mars.  The fact that rotation periods appear to be
quantised means that tidal forces cannot act in a smooth
manner, gradually changing the periods.  There must be
short periods of rapid change.

There have been other reports of the 160 minute quantum in a
variety of different phenomena.  Unfortunately I have lost the
reference for an important paper on this subject.  It gives a
method of determining a constant which is most nearly a multiple
or divisor of a set of values.  I would appreciate anyone
who has such a reference so that I can acknowledge this paper.

In summary then, many aspects of solar system formation appear
to have been strongly affected by standing waves of 80 and 160
minutes, and 3 and 6 minutes.  These waves have tightly
constrained the distances, masses and radii of all bodies,
and it is to be expected that extremely similar planets in
other systems will be found (either that of discretely different
ones).  This has a bearing on the probability of finding life
elsewhere also.

The orbital periods of the planets are also related to the
predicted universal harmonics, with most noticeably Jupiter's
11.86 year period being related (by the speed of light) to 
one of the main stellar distance quanta of 11.86 light years.
Saturn would be exactly 5/2 times this except that planets
in exact ratios disrupt each others orbits until they are
no longer so.