Harmonics of the Universe written March 1998 by Ray Tomes

The Harmonics theory has been developed over a period of many years. It is entirely my own work but there have been many confirmations of its essential validity from the work of others. The pages which follow are a description of the discoveries in time sequence. By this means I hope to show why I reached each conclusion that I did. Gradually a larger and larger picture emerges until the Harmonics theory is seen as a description of the fundamental workings of the universe.

That is not to say that it is a complete description. There is still much fundamental work to be done in arriving at what I call "The Formula for the Universe" by which I mean the field equation that makes the whole show tick. It is my opinion that such an equation will combine all the existing theories including Maxwell's equations, the Harmonics theory, General Relativity and Quantum Mechanics.

In 1977 I was using computers for economic modelling. The objective was to forecast trends in major economic variables in New Zealand and elsewhere so that my corporate customers could make better financial decisions. There are difficulties in doing this as a long and consistent historical data record is desirable for even a short term forecast. To avoid these difficulties a method called factor analysis was used to reduce the number of variables while retaining the essential information as far as possible. Factor analysis produces a small number of "factors" which not only contain most of the information about the original data but also have much of the noise removed. As such they give a clearer picture of the underlying economic processes.

Once the factors are produced another technique called regression analysis is able to produce equations which can predict from the present factors what the most likely values of them are at some future time. Finally the forecast factors can be used to "reconstitute" the original economic variables of interest. The predictions made in this way are found to be superior to many other methods. For example, when the data up until 1973 was used as a base, the model predicted a major economic contraction in 1974-75. Such an event did occur and was generally considered to be unpredictable as it was attributed to the oil price increases.

When the factor scores were plotted over the historical period it was found that some of them exhibited very regular cyclical behaviour. There was one very slow cycle of about 40 or 50 years and others of near 3, 4 and 7 years. At the time I attributed the 3 year cycle to the New Zealand election cycle and the 4 year one to the United States election cycle. My reasoning was that governments like to give people a good year before the elections and as a result need to toughen up the year after. The 7 year cycle was mainly related to New Zealand's agricultural economic base.

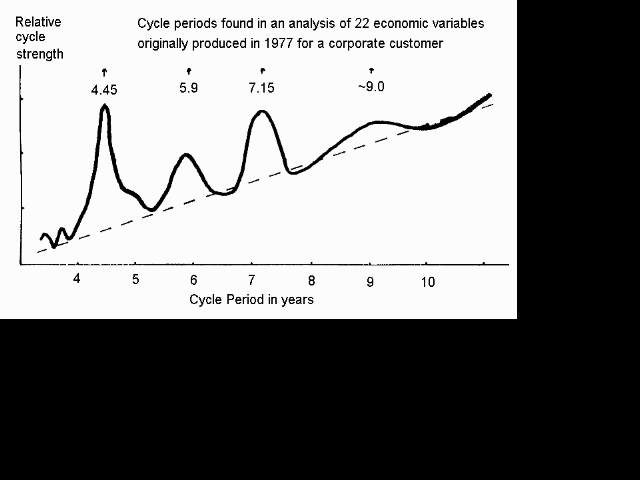
A little later I noticed that the four periods found were related in that they were all very nearly exact fractions of 35.6 years. If 35.6 years is divided by 8, 6, 5 and 4 the results are 4.45, 5.93, 7.12 and 8.9 years. In addition I had found that there was a cycle of about 12 years and that the 3 and 4 year cycles were really a tiny bit less than that. These were consistent with dividing 35.6 years by 3 to get 11.87 and by 12 and 9 to get 2.97 and 3.96 years.

What was so special about 35.6 years? I did not know the answer to that question. However I found that the long cycle had been discovered before and was called the Kondratieff cycle after its Russian discoverer. Kondratieff said that it was 54 years long and in the 1920's predicted a major depression in the 1930's. Of course he was absolutely right, and we have just completed the next depression after that one, although thankfully it was not as bad as the 1930's one. I also noticed that 108 years divided by 2 and 3 gave 54 and 36 years respectively and so it seemed that 35.6 years was connected with the Kondratieff cycle and was not some sort of special value.

As I searched for more information about cycles I came across the idea that there were some very short cycles and so I got hold of 44 years of weekly corn prices. Analysis of this data showed that there were many shorter cycles and that they had relationships to each other which were similar to the longer cycles. That is, they had many proportions involving fractions like 3/2 and 4/3 and 2. One day I noticed that the whole pattern of periods when turned into frequencies had exactly the same relationships as the frequencies of the white notes on the piano plus B flat. Then I realised that the 4:5:6:8 proportion in the economic cycles was exactly a major chord in music. Also, the corn cycles were related by factors of 2 to the economic cycles. In other words they were in the same musical key.

Was God playing major chords in the New Zealand economy and the whole scale in corn prices? It was too weird by a long way. I didn't tell many people about this as I was sure that they would think that I was crazy. I became determined to get to the bottom of cycles and to find out why these strange things happened. I had always been interested in astronomy and recognised that several of the periods that showed up were related to astronomical events. For example Jupiter's period around the sun is 11.86 years and the moon's anomalistic period (the time for its ellipse to swing around and return to the starting point) is 8.85 years which are both close to fractions of 35.6 years.

I began to see that the economy could oscillate as a result of variations in the weather and that in turn would be affected by outside influences. These influences would include the effect of the moon on rainfall due to changes in the tidal forces. Other effects would come from the sun. It was not clear how planetary periods, such as Jupiter's, could cause effects on earth unless it was through an action on the sun. I attempted to build a model whereby the planetary tidal effects on the sun would influence it but the effects were not larger enough and the model would not work. All the same, I found more cases of related planetary periods. Later this one would be solved.

Several years later I found out that there was an organisation called the Foundation for the Study of Cycles based in America. I became a member and began to receive their magazine with articles about cycles. They announced their annual conference for 1989 in California and so I went to that and to spend time in the Foundation's library where many books on cycles, including rare ones, are found.

Up until this time my journey had been as if I was the first person on a new continent. Now, for the first time, there were footprints in the sand. I saw that the path that I had been travelling had been travelled before. Almost all of my "original" ideas had been already written down by others, and all my discoveries already made. It was a source of annoyance but also a sense of comradeship. Now I knew that I was not crazy, as Edward Dewey who had started the Foundation many years before had published a table of common cycle periods related by factors of 2 and 3 and there sitting near the middle was a period of 35.5 years!

Dewey had periods of 35.5, 8.88, 5.92 and 4.44 years which agreed very well with my figures. Given that his research was based on entirely different data to mine, being from different countries, different time periods and different variables, it was now possible to be very confident that the pattern was a real persistent feature of life on earth and probably beyond. He had also looked at the astronomical connections and found that when the sunspot cycle was plotted with the N-S polarity include that there was a period of 17.92 years present in addition to the well known 11 or 22 year period. This was close to 35.6 years divided by 2. Dewey had collated thousands of reports of cycles in everything that you can imagine and these were published by the foundation in a four volume set "Cycles Classic Library Collection" along with many of his articles about cycles.

Even the musical relationships in cycle periods had been found before by D S Castle, who in 1956 wrote an article "Stock Market Cycles Fit the Musical Scale".

How could cycles with related periods come about? Dewey had written that he felt like Tycho Brahe who collected the best ever data on the planetary positions but was unable to solve the problem of the planets' orbits. He had to wait for Kepler to do it using Brahe's data. In his late years Dewey said the he had resigned himself to the same fate but hoped that someone would use his research to solve the riddle of the related periods. He had also discovered that for each individual cycle period most of the cycles had peaks at nearly the same time. A few were exactly opposite but the phases of the often diverse variables were not random. He called this cycle synchronies.

The economy could be affected by variations in commodity prices. Many commodities are either crops or animal products which are both affected by the weather. For any given crop there is an optimum set of weather conditions for a good crop. Too much rain is a problem just as too little is. Crops are generally grown in an environment that is right on average. So if there was for example a 12 year cycle in rainfall it could well be that for some crop this included periods of too much and too little rain. In that case the yields would follow a 6 year cycle, being poor at the extreme rainfall limits and good in between. In practice it is unlikely that both extremes would be equally severe so that a likely result is a 6 year cycle superimposed on a 12 year cycle.

Just this sort of pattern is observed for some variables. For example the 4.45 year cycle is a slowdown in the economy. However every alternate slowdown tends to be more severe which is why the 8.9 year cycle exists.

The sort of behaviour described above is a non-linear system. It means simply that equal variations in one thing do not cause equal variations in something else. All sorts of variations in the relationships are possible, but it always results in periods which are exact fractions of the original cycle. So for example a 35.6 year cycle in something which affects many things could produce cycles of 17.8, 11.87, 8.9, 7.12, 5.93, 5.14, 4.45, 3.96 years and so on. Likewise a cycle of about 108 years could produce cycles of 54 and 36 years. It seemed clear that non-linear systems played an important part in the whole mystery.

These cycles of fractional periods are called harmonics of the original cycle. However it was clear that not all harmonics were created equal. For example the 5.14 year cycle was not commonly reported. It is the 7th harmonic. However harmonics with lots of factors of 2 and 3 were reported very often. What was so special about them?

Although it is normal to use periods for slow cycles and frequencies for fast ones, it will be found much more convenient to use frequencies when talking about harmonics as then everything comes out as 1, 2, 3, 4 ... rather than 1, .5, .3333, .25 ... which can get messy.

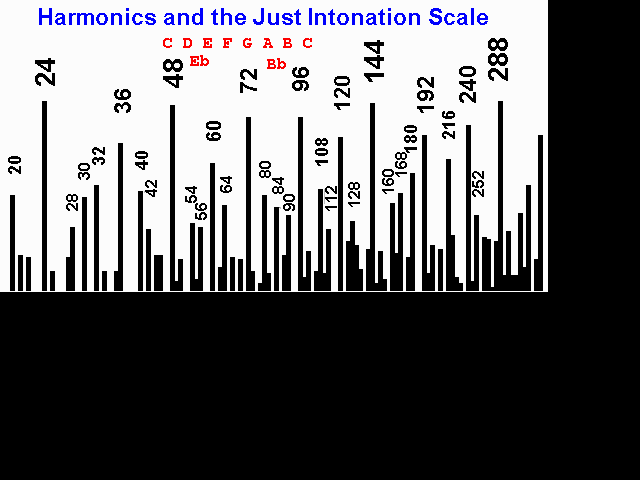
Going back to the musical scale, I eventually worked out the relationships between the frequencies which corresponded to the old just intonation scale. This was in common use in music until Bach and others popularised the equitempered scale which is now used for most fixed tuning instruments. The just intonation scale has frequencies for the scale in the proportions 24, 27, 30, 32, 36, 40, 45, 48. These numbers all have lots of factors of 2 and 3 and sometimes one factor of 5. This was the pattern that I had found in the corn prices.

One of the points about the musical scale is that it fits together in lots of ways. For example the values 24, 30, 36, 40 are in the proportions 4:5:6:8 and make a major chord. So to, the values 32, 40, 48 are a major chord. In fact the scale is nothing other than 3 major chords stuck together. It is the multitude of relationships which gives the clue about how the observed cycle's pattern develops.

Suppose that we had one very long cycle in something which affected many other things. Suppose also that the relationships were all non-linear and so developed harmonics. Also assume that each of these things proceeds to do the same. What is the result?

This table shows the harmonics produced starting from 1 and continuing with its harmonics.

1  -->      2  3  4  5  6  7  8  9  10  11  12  13 ...
2  -->            4     6     8     10      12
3  -->                  6        9          12
4  -->                        8             12
5  -->                              10
6  -->                                      12
...etc

If we carry this on a bit further we will find that the pattern begins to look very much like the just intonation music scale. The pattern of strong harmonics from 48 to 96 is exactly the same as doubling the just intonation scale figures above. Not only that, the next strongest harmonics are some of the black notes, especially B flat and E flat. The very strongest ones are the major chord itself.

Using a computer I have calculated the relative power in the harmonics out to very high order harmonics.

This graph shows the strong harmonics up to a million shows the pattern and the variations in it. The numbered harmonics in the graph are the ones which I call the "main line" because they are the strongest ones and they are related by ratios of prime numbers. This calculation when continued to very high order appears to describe many aspects of the structure of the universe.

A number of quite mysterious behaviours have been found to be explainable in a way that has removed much of the mystery. There are clearly still some questions. Let us first take stock of what has been discovered and what has been explained.

Cycles have been observed in everything. Not all of these observations are real. Some are just due to noise happening to make patterns for a while. However when much data from different fields of study are brought together it is clear that there are certain cycle periods which are real and which occur quite commonly. In addition these periods are related to each other harmonically in exactly the same way that musical notes are.

Starting from a single low frequency, non-linear systems can generate harmonics which are multiples of that frequency. In a complex system, which the universe and world certainly are, under certain conditions it seems that the harmonics generated may take on a life of their own and proceed to generate further harmonics of their own frequency. Once this happens some frequencies will be produced in many more ways than others. These frequencies are the ones that are harmonics of the original where the harmonic number has many ways to be factorised such as 12 and 24 and the just intonation scale of 48, 54, 60, 64, 72, 80, 90, 96.

An expanded portion of the predicted harmonics spectrum is shown and how this relates to the just intonation music scale.

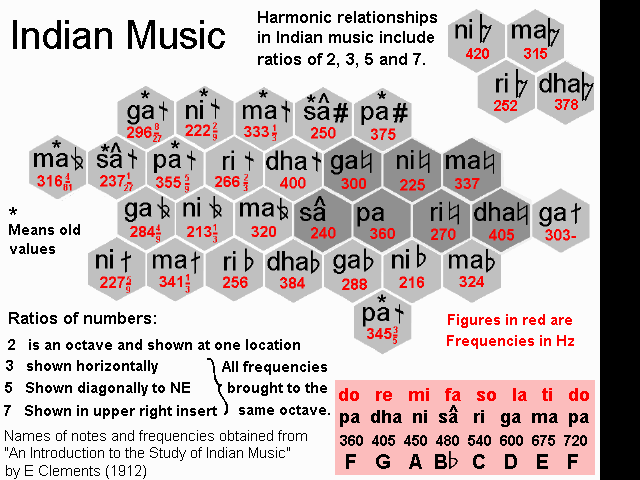
 It is interesting to compare this structure to the pattern of frequencies used in Indian music.

There is one difficult point in the above which needs to be raised. How does a particular frequency "take on a life of its own"? What do I mean by this? I mean that when the non-linear system generated many frequencies these have to somehow get separated out from each other or else they cannot become the starting point for the generation of new harmonics in their own right. There are several possible ways in which this might happen. For now I will confine the discussion to the first one that occurred to me. To do that requires a brief look at how resonance works first.

Many things in the real world have some sort of natural oscillation period. For example a swing. If we push it repeatedly at the right intervals we can get a large oscillation to build up gradually. If we push it at the wrong intervals we will only get small oscillations. The same sort of thing happens in very many systems. Of course our old friends the musical instruments come to mind again. An instrument will respond to a note played which is near to the instruments natural frequency. Musicians will all have experienced the odd household item such as light fittings, glasses and vases which hum when a certain note is played.

Resonance is characterised by the frequency of the resonance and by its sharpness. A sharp resonance will only respond to a frequency very near the natural frequency but is then capable of a very prominent response. The object will ring. Musical instruments have sharp resonances. So do pendulum clocks. When several pendulum clocks are mounted on the same wall, the tiny vibrations sent through the wall are sufficient for them to get into exact step and keep identical time over long periods.

Not only physical objects have resonance. What we might regard as abstract systems may also have resonance. Suppose that the price of sugar is high. This leads more people to be tempted to grow sugar. After a while the extra sugar being grown will, through the law of supply and demand, cause the price to begin to fall. Unfortunately for the growers they have still got much more in the fields. When this comes in there is then a glut and the prices go very low. Some growers decide to grow something else. After a while the reduced supply begins to cause the price to move upwards. Here we go again!

The above description applies to all commodities and manufactured goods and services also. The main thing which varies from one situation to the next is the period of time that it takes to complete a cycle. In the case of sugar it is about 6 years. The price of sugar at the peaks is typically about 300% to 500% higher than at the troughs. It is therefore the case that sugar prices have a resonance of period about 6 years and that it is quite a sharp resonance.

The behaviour of economic cycles in general can be explained quite well by resonance. If that was the only factor however then each system would have its own unique cycle period. We know that that is not the case. All the periods are harmonically related. This could come about in part because there are effects between the different commodities. The price of ice-cream will depend on the prices of both milk and sugar. The demand for ice-cream will depend on its price and so to at least some extent the demand for milk will depend on the price of sugar. These effects are small but sufficient to cause cycles which are nearly harmonically related to become exactly so. Just like the clocks ticking together.

I don't know the correct figure, so let us suppose the natural cycle for sugar booms and busts is exactly 6 years. Suppose also that there is something which affects sugar demand by having a non-linear variation of period 17.8 years. In that case it is easy to imagine that the sugar price will vary with a period of exactly 5.93 years as the 3rd harmonic of the 17.8 year period will match the sugar resonance at 6 years closely enough to get a good strong swing in prices going.

This process is like the little graphic equaliser settings on many stereos. If just one band is selected and the rest turned down, what we hear is just the notes and harmonics which are in the range selected. In the case of sugar it is the 5.93 year "note" which gets through.

Sugar is a particularly sharp resonance, and others are less so. For example the stock market allows several harmonics of the 17.8 year period through its graphic equaliser. Both the 4.45 and 5.93 year periods are found in the Stock Market. The shorter one is stronger and so we may suppose that the natural period is less than 5 years.

For some systems the natural period changes with time. Changing technology and communications may speed things up while increased bureaucracy might slow them down. If only harmonics of certain periods are allowed to show, these structural changes will manifest themselves as a gradual fading of one frequency and a build up of another. However the in between frequencies will not show up at all.

The change above is in some ways similar to the quantum changes in atoms which jump from one frequency to another without showing the in between frequencies at all. Perhaps they only appear to jump because they are so fast but in fact one fades out and the other fades in over a small time interval.

Anyway, I am getting ahead of myself. More about that later. For now it is sufficient that a possible cause has been established for frequencies being singled out in the real world. As such they can then be the seeds for developing more harmonics as the processes are almost certainly non-linear.

The above description has been given for economic systems, but exactly the same principles apply for other systems. Astronomical systems will respond to external oscillations also. For example a cloud of dust being affected by a repeated non-linear force will separate into rings with orbital periods which match the harmonics of the forcing period. Clearly such a mechanism would lead to some definite order in planetary systems as an example.

Dewey's chart of common cycles only included ratios of 2 and 3 and products of these. If the harmonics theory is correct then there should be the occasional ratio of 5 and 7 also. There was a ratio of 5 observed with the 7.15 year period being near to 1/5th of the 35.6 year period. There are several extra groups of cycles which did not fit Dewey's original scheme but which do fit when ratios of 5 and 7 are considered.

Most notably, 5 times 35.6 years gives 178 years. This period is mentioned by many cycles researchers and has been associated with climate, the sun, planetary alignments and earthquakes. The data for some of these are contentious. There is certainly a common interval of 178.7 years between rough alignments of the 4 major planets with the sun. The presence of this cycle in the climate is reported along with nearly 60 year and nearly 20 year cycles. The last one is well known as the cycle of droughts in the American mid-west where it causes failure of the crops. These three periods are of course related by ratios of 3's.

The two largest planets, Jupiter and Saturn, go past each other on average every 19.86 years as they orbit the sun. This happens in the same part of the sky every third time, or every 59.6 years. Every third time that this occurs Uranus has completed two orbits and Neptune one and so all four get nearly together. Over a longer cycle of 2300 years these alignments get better and worse. Interesting the 2300 year cycle is also often reported as a major climatic cycle. It certainly seems that the major planets are influencing the climate, probably through an effect on the sun which then affects us.

If we repeatedly divide 178 years by 2 we get the sequence 89, 44.5, 22.2, 11.1 years. The moon's orbit has two factors which come together every 89 years. The sunspot cycle is generally called an 11.1 year cycle, although really it is a 22.2 year cycle when the reversal of its north and south poles is included. One third of 89 years is 29.6 which is very close to Saturn’s orbital period. So there are many astronomical periods in the group of cycles which are 5 times the 35.6 year group. Some of these are observed on earth also.

Most of the shorter cycles found by Dewey fitted into his proportions of 2 and 3 from 17.75 years. One major exception is the so-called 40 month cycle. This has been determined accurately by the Foundation as being 40.68 months or 3.39 years. This divides into 35.6 years 10.50 times and so is not a harmonic. However if we use 71.2 years (35.5 x 2) as a starting point then 3.39 years is the 21st harmonic. Of course 21 is 3x7 and so here is a factor of 7.

The sceptical element of the physics community will say that this is numerology. However later we will demonstrate that the observed cycles do very accurately fit the predicted pattern. In the mean time we need to know what is the pattern. If the factor of 21 above is just numerology then there is no reason for other cycles to be observed that relate to this by the usual proportions of 2 and 3. However there are many shorter cycles that do relate. There is a 10 month cycle in the stock market, which is 1/4 of 40 months. At 1/8th of 3.39 years we get 0.424 years or 155 days. A 155 day cycle and another of half this have been reported for various solar phenomena. Dividing by 3 (from the half of 155 days) gives a period of 25.8 days which is the solar rotation period at the equator. So there is a reasonable body of evidence for a set of shorter cycles at 1/7th of the 35.6 year set.

In summary then, there are three groups of cycles with many ratios of 2 and 3 between them and these three groups are related by a ratio of 5 between the long cycles and the medium length ones and a ratio of 7 between the medium ones and the shorter cycles. In my estimation more than 95% of all commonly reported cycles from every branch of knowledge fit this pattern in the range of one week through to several hundred years.

It is clearly desirable to try and fit the pattern observed to the theoretical pattern predicted by the harmonics theory. If the theory is correct then there will be a single period which is the "number one cycle" and all the other periods will follow from this based only on the properties of numbers.

There is one disturbing observation in attempting to do this. It is that there appears to be another family of cycles from 2300 years upwards. Both 2300 and 4600 years are reported as climate cycles and they also exist in the solar system as giant planetary periods. Specifically, good conjunctions of the four giant planets can only occur in the favourable part of this cycle which has a period of 2315 years. There also appears to be a 55,500 year cycle in the motions of the planetary orbits relative to each other. That period is 24 times 2315 years which makes it a member of the same family.

I mentioned a problem. It is that 2315 years divided by 178 years is 13.00 almost exactly. It reminds me of the response to the discovery of the mu meson, "who ordered that?" If the harmonics theory is correct then a ratio of 13 should not occur until quite a small fraction of the full cycle of the universe. If the 13 is real and the harmonics theory correct then the universe must be much bigger than expected and have a very much longer cycle. So I decided that as the evidence for this ratio was not quite as strong as the others I would ignore the 13 ratio for now and see what happened.

The theory said that the first ratio of 7 should occur at a slightly longer period than the second ratio of 5. However we find these two the other way around. If these ratios were the second ratio of 5 coming down from the size of the universe then the first one would bring us to the scale of galaxies and the second one to the scale of stars. I convinced myself that because galaxies rotate the effects of universal waves would get out of phase with the galactic waves. In this way it made sense that the stellar sized waves would partly look like we had started again from galaxy sized waves and partly that we had continued from the universal waves. So the factor of 7 would be delayed.

Based on this I worked backwards from the 35.6 year group of periods and determined the "number one cycle" period to most likely be 14.17 billion years. It was distinctly possible that this would be out by a factor of 2 either way or perhaps 3/2 or 4/3. A longest cycle of 14.17 billion years after division by 34560 two times would give a cycle of 11.86 years which is Jupiter's period. Three times this is 35.6 years, which is where I began from.

If the longest cycle were 14.17 billion years then the 24th harmonic ought to be a very noticeable one at 590 million years. Repeated division of this period by 2 gives periods of 295, 148, 73.8 and 36.9 million years. On one of my many trips to the Auckland University library I came across the book "Megacycles" edited by G Williams. He is an Australian geologist who has made studies of cycles in geological formations and I had previously come across his work in papers dealing with cycles that seemed to show the sunspot cycle in rocks which were formed 700 million years ago.

In "Megacycles" Williams reported that there was evidence of a series of geological cycles with periods 37, 74, 150, 300 and 600 million years. He considered that these were associated with astronomical cycles which continued to 1200 million years. The agreement between these figures and the predictions of the harmonics theory were excellent. It seemed to be working.

Not everything fitted however. Based on the 14.17 billion year cycle the 34560 harmonic was predicted to be very prominent and this came to 410,000 years. This also meant that there should be a galaxy distance quantum of 410,000 light years. The 2880 harmonic would also produce another prominent distance of 4.92 million light years. These figures were reasonable for galaxy distances, but the indications were that many galaxies are at distances of about 2.2 million light years, with a smaller quantum for the smaller satellite galaxies such as the Magellanic clouds.

Furthermore there is a calculated period of 1.11 million years for energy exchange between some of the outer planets. This could be linked to the 2.2 million light year distances by a factor of 2 and also to the 111,000 and 55,500 year orbital changes which I knew already linked to the 4600 and 2300 year periods. So there was an island of periods that didn't link to the continents on either side. This would remain as a nagging doubt.

According to the prevailing view of the universe, the big bang is responsible for the galaxies all flying apart at great velocities. The velocities are supposedly proportional to the distances between the galaxies and related by the Hubble constant. The constant is named after Edwin Hubble who discovered that galaxies have redshifts in proportion to their distances.

If the galaxies are moving away from each other with velocities that are all multiples of 72 km/s then something very, very strange is going on. For a start, when a third galaxy is considered, it must also be moving away from the original two at a multiple of 72 km/s. How does this work if the triangle so formed is not equilateral. Something has got to give.

Anyway, taking the 72 km/s redshift as a fraction of the speed of light gave a figure of 1/4160. If it had come out to 1/2880 then I would have been delighted. I must have put these figures into my calculator a hundred times, but it always said 1/4160 and never 1/2880. What was going on here? The ratio between these two is 0.69 which meant nothing to me.

Eventually it came to me. There should be a giant wave in the universe and it ought to be divided up into 2880 and 34560 parts. However it didn't matter how many galaxy steps we looked out, the apparent recession velocity would never get to the speed of light. That is because in relativity you can add 72 km/s together as many times as you like and never get to c. So my dividing 72 km/s into c was a mistake. The number 4160 meant nothing.

So what would the redshift be from one end of the "number one wave" to the other? The answer lies in finding a wave which is most stable over a long time period. There are two competing effects on the frequency of light. One is the redshift, which is making frequencies get lower with time. The other is the development of harmonics which is causing energy to be transferred to higher frequencies. If these two forces were in balance then there would be a sort of dynamic equilibrium. This equilibrium would occur between the redshift and the 2nd harmonic because most of the energy lost from a wave goes to the second harmonic.

Astronomers measure redshifts as z values. The value of z is the change in wavelength as a fraction of the original wavelength. So if z=0.2 then all wavelengths have got 20% longer and if z=1 then all wavelengths have doubled. If the number one wave has lost energy to the second harmonic then it will be returned to the original wavelength over a distance at which z=1. Therefore the 2880 harmonic of this will be 1/2880 of that distance and the redshift at that distance will satisfy (1+z)2880=2. This gives z=.0002407 and zc=72.15 km/s. At last it fits. This confirmed that the number one wave had a wavelength over which z=1.

Based on this agreement it was possible to predict many more redshift quanta. There should be very many different waves that play a part in galaxy formation and these should be able to be detected as redshift periodicities. At the time that I came to this understanding I knew of only one redshift quantum that had been observed. So I made a list of predicted quanta and posted this list to usenet (a part of internet) with my stated intention to analyse a galaxy survey to test the prediction. However I received a reply stating that I should check out the work of W G Tifft who had made a study of redshifts.

When I found Tifft's 1978 paper I was amazed. He had already discovered nearly all the smaller redshift quanta from my list. In his later papers and as a result of contacting him personally I was able to make a list of redshift quanta that he had observed. The agreement was extremely statistically significant and it could not be seriously doubted that Tifft's observations and the Harmonics theory were in agreement and were both saying something important about the structure of the real universe.

Surprisingly, the redshift quantisations can be calculated to unlimited accuracy without knowing the Hubble constant. This is because they are really made in units of z which does not depend on our human measurement scales. Normally astronomers quote redshifts in velocity units, which means that they accept that the redshifts are 100% caused by the Doppler effect. This practice has been criticised by astronomer Halton Arp and I agree with him. Redshift quantisations should be quoted in units of delta(log(1+z)). That is the basis on which they are truly constant over long distances and it does not beg the question of the redshift interpretation.

The detailed predictions of the Harmonics theory for the strongest redshift periodicities are shown in graphic form. For large redshift periodicities the value of delta(ln(1+z)) are shown while for smaller ones the more commonly used values of zc are shown.

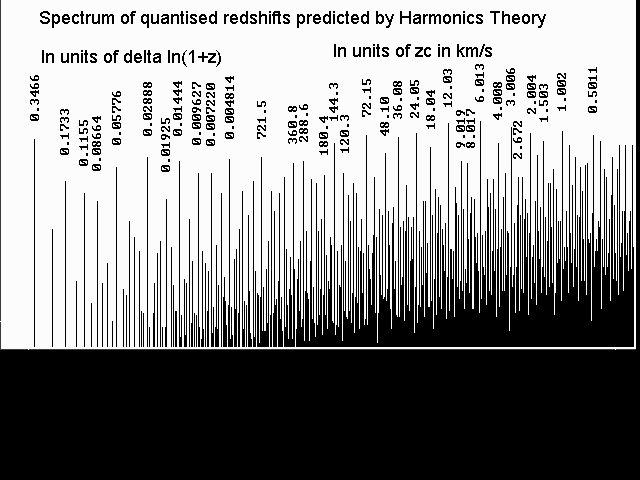
For comparison, from the various reports of W G Tifft plus a private communication the list of observed values are 144, 72, 36, 24, 18, 16, 9.0, 8.0, 6.0, 3.0 and 2.67 km/s.

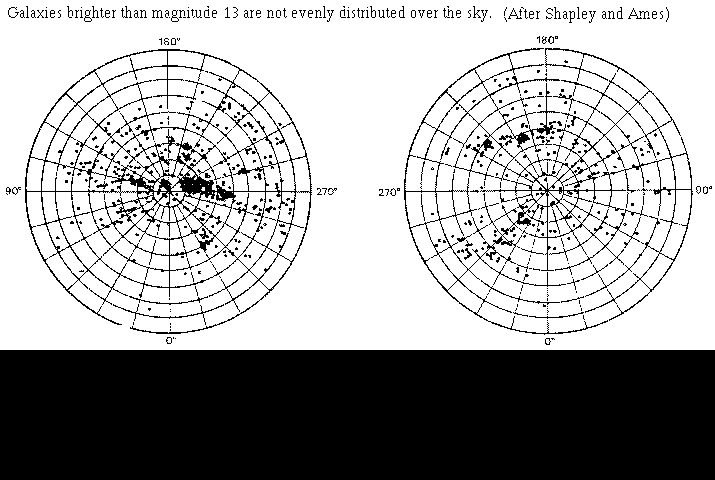
Most people know that the bright stars are mostly arranged as a broad band across the sky. Even many astronomers are not aware however that the bright galaxies are similarly arranged.

The Hubble constant is defined so that (1+z) = e^(Hx/c) where x is the distance, H is the Hubble constant and c the speed of light. Substituting z=1 and x=14.17 billion light years gives H=ln(2).c/14.17e9 light years or H=1/20.44e9 years. Usually H is given in some rather strange astronomer units of km/s per megaparsec. As mentioned this is a bad practice because it assumes that redshifts are velocity caused. Anyway the answer is that H=47.8 km/s/Mpc. As mentioned before, it is possible that this value is out by a factor of 2 or even 4/3 or 3/2, but unlikely.

The Hubble constant has been very difficult to establish accurately. Measurements range from about 30 to 100 km/s/Mpc with two groups favouring very different values of around 50 and around 85. Recent measurements by Sandage using the 200" telescope have been mainly between 45 and 50 and so agree well with my value.

Measurements are usually claimed to be uncertain by 15% or more, although not many astronomers would bet their lives without at least a 50% margin. The value of 47.8 should be accurate to 0.2% if the harmonics have been correctly identified, otherwise it will be totally wrong. As measurements improve it should be possible to become sure that the correct harmonic identification has been made and the harmonics theory will then provide a much improved distance scale for the universe.

Unfortunately only the distances to the very nearby star are known to any accuracy. Soon many more stars will have more accurate distances but it is only possible to use the available data. The expected result of the Harmonics theory is that stellar distances in light years will tend to be multiples of the common cycle periods in years. I performed two tests.

Firstly I calculated the distances between every pair of stars among the nearby ones to increase the number of distances in the sample. The resulting histogram was compared to the expected histogram based on a regular cubic grid. It was very similar, and the unit of the grid derived in this way was 4.43 light years. This compares to Dewey’s 4.44 year and my 4.45 year cycles. The histogram had more star pairs at distances corresponding to all the common cycle periods, 4.45, 5.93, 7.12, 8.9, 9.6, 11.86 light years. Even though the data was lacking in quantity it gave support to the Harmonics theory.

The second test was to see if a cubic grid of 4.44 light years would fit the data. This was tested by examining the extent to which the stars lay on planes 4.44 light years apart for every possible orientation of the planes. The result was that three directions were found for which the planes had almost all the stars in them and they were near to orthoginal. The few stars which did not fall near the planes where mainly halfway in between. A large proportion of the stars fell on alternate planes and so belonged to a 8.88 light year grid.

There is a good reason why the stellar planes should not be exactly orthoginal. It is that such an arrangement would make many stars be at distances which are the square root of 2 units apart. The square root of 2 is 1.414... and does not fit the harmonics pattern. However a rhombus with sides of length 1 and twisted just a little from a square will have diagonals which are very close to 3/2 and 4/3. As these are good harmonic relationships, this is clearly a better arrangement to satisfy all the harmonics simultaneously. Interestingly the error in this rhombus is just 1 part in 288 from satisfying the 3 conditions simultaneously.

Return to Ray Tomes index page